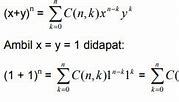Deskripsi Proyek Secara Detail
Proyek ini akan dilakukan oleh kelompok yang terdiri dari 3 hingga 5 siswa, di mana tiap kelompok akan diberi tugas untuk menyelesaikan sejumlah soal ekspansi binomial, menghitung jumlah koefisien untuk tiap soal, dan akhirnya mendiskusikan relevansi dan aplikasi dari konsep ini.
Semua kelompok akan menerima sejumlah soal ekspansi binomial dan harus bekerja sama untuk menyelesaikannya.
Langkah-langkah Detail untuk Melakukan Aktivitas
Setelah menyelesaikan bagian praktis, setiap kelompok harus membuat laporan tertulis yang mencakup topik-topik berikut:
Siswa harus membuat kontekstualisasi dari topik "Jumlah Koefisien Binomial" dan relevansinya di dunia nyata. Selain itu, tujuan dari proyek ini harus dinyatakan dengan jelas.
Di bagian ini, siswa harus menjabarkan teori "Jumlah Koefisien Binomial". Mereka harus menjelaskan aktivitas yang dilakukan secara detail, menunjukkan metodologi yang digunakan dan terakhir, menyajikan dan mendiskusikan hasil yang didapat.
Siswa harus merefleksikan tentang pembelajaran utama yang didapat selama proyek dan aplikasi praktis dari teori yang dipelajari. Penting bagi siswa untuk tidak hanya menunjukkan penyelesaian masalah, tetapi juga bagaimana mereka bekerja sama untuk mencapai hasil.
Siswa harus mengutip semua sumber informasi yang digunakan untuk mempersiapkan proyek. Ini termasuk buku, situs web, video, dan lain-lain.
Laporan final harus diserahkan seminggu dari tanggal dimulainya proyek.
Ekspresi dua suku (dua variabel atau satu variabel dan satu bilangan) seperti $(x+y)$, $(a-2x)$, atau $(3x-10)$ disebut binomial. Bentuk $\displaystyle \binom{n}{k}$ (baca: $n$ pilih $k$, dalam bahasa Inggris, $n$ choose $k$) disebut koefisien binomial karena koefisien-koefisien tersebut memenuhi teorema binomial berikut ini. Teorema binomial ini seharusnya sudah dipakai oleh siswa SMA ketika membahas materi yang berkenaan dengan aljabar.
Misalkan $x$ dan $y$ adalah variabel serta $n$ merupakan suatu bilangan bulat nonnegatif. $$\begin{aligned} (x+y)^n & = \displaystyle \sum_{j=0}^n \binom{n}{j} x^{n-j}y^j \\ & = \binom{n}{0}x^n + \binom{n}{1}x^{n-1}y + \cdots + \binom{n}{n-1}xy^{n-1} + \binom{n}{n}y^n \end{aligned}$$
Kita akan menggunakan pembuktian kombinatorial. Jika dijabarkan, suku-suku hasil perkaliannya berbentuk $x^{n-j}y^j$ untuk $j = 0, 1, 2, \cdots, n.$ Untuk menghitung banyaknya suku berbentuk $x^{n-j}y^j$, perhatikan bahwa kita perlu memilih $(n-j)$ variabel $x$ dari penjumlahan $n$ suku tersebut sehingga kita juga secara otomatis memilih $j$ variabel $y.$ Oleh karena itu, koefisien dari $x^{n-j}y^{j}$ adalah $\displaystyle \binom{n}{n-j}$ yang senilai dengan $\displaystyle \binom{n}{j}.$ Dengan demikian, teorema binomial tersebut terbukti benar. $\blacksquare$
Ketika kita mengambil $n = 2, 3, 4$, kita memperoleh rumus binomial yang sangat sering dimunculkan di sekolah menengah, yaitu $$\begin{aligned} (x+y)^2 & = x^2+2xy + y^2 \\ (x+y)^3 & = x^3+3x^2y + 3xy^2 + y^3 \\ (x+y)^4 & = x^4+4x^3y+6x^2y^2+4xy^3+y^4. \end{aligned}$$Jika diperhatikan secara saksama, koefisien dari setiap suku sama dengan bilangan yang ada pada baris-baris Segitiga Pascal. Dari sini dapat ditunjukkan bahwa proses pembentukan bilangan dari Segitiga Pascal dengan menjumlahkan dua bilangan di atasnya adalah benar.
Beberapa poin penting yang perlu diketahui dari submateri kombinatorika ini adalah sebagai berikut.
Penjelasan singkat di atas merupakan ringkasan penting mengenai teorema binomial. Pembaca sebelumnya diharapkan sudah memahami teori yang lebih rinci di buku teks. Pada pos ini, kita akan membahas beberapa soal terkait teorema binomial. Soal juga dapat diunduh dengan mengklik tautan berikut: Download (PDF, 160 KB).
Kali ini kita akan membahas materi selanjutnya yaitu tentang Binomial Newton. Salah satu materi penting dalam Peluang yang akan kita bahas selanjutnya.
Binomial Newton adalah teorema yang menjelaskan mengenai pengembangan eksponen dari penjumlahan antara dua variabel (binomial).
Dalam Binomial Newton menggunakan koefisien-koefisien
Untuk n = 2 diperoleh :
Untuk n = 3 diperoleh :
untuk mempermudah kita dalam menetukan koefisien binomial, maka dapat digunakan dengan konsep kombinasi yang dikenal dengan Binomial Newton atau Ekspansi Binomial.
Rumus Binomial Newton dinyatakan sebagai berikut:
dengan n dan k adalah bilangan asli.
Untuk mempermudah pemahaman kalian tentang Notasi Sigma dan Kombinasi , silahkan dibaca link berikut:
Menentukan Koefisien dan Suku Binomial Newton
Dalam menentukan koefisien dan suku Binomial Newton dapat diperoleh dengan cara:
Jika yang ditanya adalah suku ke-m dari hasil penjabaran di atas dapat ditentukan dengan rumus:
Ingat saja: Jika ditanya suku ke-m maka kurangi 1 jadi m-1
Jadi, koefisein suku ke 7 adalah 2.562.560
Blog Koma – Sebelumnya kita telah belajar materi “Kombinasi pada Peluang dan Contohnya” yang merupakan bagian dari kaidah pencacahan. Ternyata konsep kombinasi bisa dikembangkan pada pembahasan Binomial. Pada artikel kali ini kita akan membahas lebih spesipik tentang Konsep Binomial Newton (Ekspansi Newton). Binomial Newton mempelajari tentang cara penjabaran(ekspansi) bentuk pangkat aljabar yang terdiri dari dua suku (binomial).
Untuk menjabarkan bentuk pangkat aljabar dua suku bisa menggunakan sigitiga Pascal seperti berikut ini :
Dari bentuk segitiga pascal tersebut dapat membantu dalam penjabaran pangkat dua suku berikut dimana angka-angka pada segitiga pascal merupakan koefisien dari setiap sukunya: $ \begin{align} (a+b)^0 & = 1 \\ (a+b)^1 & = a + b \\ (a+b)^2 & = a^2 + 2ab + b^2 \\ (a+b)^3 & = a^3 + 3a^2b + 3ab^2 + b^3 \\ (a+b)^4 & = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + y^4 \\ (a+b)^5 & = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5 \\ (a+b)^n & = ….. \end{align} $
Tetapi ada metode lain yang lebih mudah diterapkan untuk mencari koefisien binomial yaitu dengan menggunakan Konsep kombinasi $ C_r^n \, $ yang dinamakan Binomial Newton (Ekspansi Binomial), sehingga segitiga pascal dapat ditulis sebagai berikut.
Contoh Soal Binomial Newton (Ekspansi Binomial) :
Untuk memudahkan menghitung bentuk kombinasi, silahkan baca materi kombinasi pada artikel “kombinasi pada peluang“.
1). Jabarkan bentuk binomial berikut ini: a). $ (x+2)^4 $ b). $ (2a + 3b)^3 $ c). $ (a – 2b)^3 $ d). $ \left( x + \frac{2}{x} \right)^5 $ Penyelesaian : a). $ (x+2)^4 \, $ artinya $ n = 4 $ $ \begin{align} (a+b)^n & = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \\ (x+2)^4 & = \displaystyle \sum_{r=0}^4 C_r^4 x^{4-r}2^r \\ & = C_0^4 x^{4-0}2^0 + C_1^4 x^{4-1}2^1 + C_2^4 x^{4-2}2^2 + C_3^4 x^{4-3}2^3 + C_4^4 x^{4-4}2^4 \\ & = 1. x^{4}.1 + 4. x^{3}.2 + 6. x^{2}.4 + 4. x^{1}.8 + 1. x^{0}.16 \\ (x+2)^4 & = x^{4} + 8x^{3} + 24 x^{2} + 32x + 16 \end{align} $
b). $ (2a + 3b)^3 \, $ artinya $ n = 3 $ $ \begin{align} (x+y)^n & = \displaystyle \sum_{r=0}^n C_r^n x^{n-r}y^r \\ (2a + 3b)^3 & = \displaystyle \sum_{r=0}^3 C_r^3 (2a)^{3-r}(3b)^r \\ & = C_0^3 (2a)^{3-0}(3b)^0 + C_1^3 (2a)^{3-1}(3b)^1 + C_2^3 (2a)^{3-2}(3b)^2 + C_3^3 (2a)^{3-3}(3b)^3 \\ & = 1. (2a)^{3} .1 + 3. (2a)^{2}(3b) + 3. (2a)^{1}(3b)^2 + 1. (2a)^{0}(3b)^3 \\ & = 1. 2^3.a^3 .1 + 3. 2^2.a^2.(3b) + 3. (2a).3^2.b^2 + 1. 1.3^3.b^3 \\ (2a + 3b)^3 & = 8a^3 + 36a^2b + 54ab^2 + 27b^3 \end{align} $
c). $ (a – 2b)^3 \, $ artinya $ n = 3 $ $ \begin{align} (x+y)^n & = \displaystyle \sum_{r=0}^n C_r^n x^{n-r}y^r \\ (a-2b)^3 & = (a + (-2b))^3 \displaystyle \sum_{r=0}^3 C_r^3 a^{3-r}(-2b)^r \\ & = C_0^3 a^{3-0}(-2b)^0 + C_1^3 a^{3-1}(-2b)^1 + C_2^3 a^{3-2}(-2b)^2 + C_3^3 a^{3-3}(-2b)^3 \\ & = 1. a^{3}.1 + 3. a^{2}(-2b) + 3. a^{1}(-2b)^2 + 1. a^{0}(-2b)^3 \\ & = a^{3} + 3. a^{2}(-2b) + 3. a.(-2)^2.b^2 + 1. 1.(-2)^3.b^3 \\ (a-2b)^3 & = a^{3} -6a^2b + 12ab^2 -8b^3 \end{align} $
d). $ \left( x + \frac{2}{x} \right)^5 \, $ artinya $ n = 5 $ $ \begin{align} (a+b)^n & = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \\ \left( x + \frac{2}{x} \right)^5 & = \displaystyle \sum_{r=0}^5 C_r^5 x^{5-r} \left( \frac{2}{x} \right)^r \\ & = C_0^5 x^{5-0} \left( \frac{2}{x} \right)^0 + C_1^5 x^{5-1} \left( \frac{2}{x} \right)^1 + C_2^5 x^{5-2} \left( \frac{2}{x} \right)^2 \\ & + C_3^5 x^{5-3} \left( \frac{2}{x} \right)^3 + C_4^5 x^{5-4} \left( \frac{2}{x} \right)^4 + C_5^5 x^{5-5} \left( \frac{2}{x} \right)^5 \\ & = 1. x^{5} .1 + 5. x^{4} \left( \frac{2}{x} \right) + 10. x^{3} \left( \frac{2^2}{x^2} \right) \\ & + 10. x^{2} \left( \frac{2^3}{x^3} \right) + 5. x^{1} \left( \frac{2^4}{x^4} \right) + 1. x^{0} \left( \frac{2^5}{x^5} \right) \\ & = x^5 + 5. x^{4} \left( \frac{2}{x} \right) + 10. x^{3} \left( \frac{4}{x^2} \right) \\ & + 10. x^{2} \left( \frac{8}{x^3} \right) + 5. x^{1} \left( \frac{16}{x^4} \right) + 1. x^{0} \left( \frac{32}{x^5} \right) \\ & = x^5 + 10 x^{3} + 40 x^{1} \\ & + 80 \left( \frac{1}{x} \right) + 80 \left( \frac{1}{x^3} \right) + \left( \frac{32}{x^5} \right) \\ \left( x + \frac{2}{x} \right)^5 & = x^5 + 10 x^{3} + 40 x + \frac{80}{x} + \frac{80}{x^3} + \frac{32}{x^5} \end{align} $
Ngerti materi denganTanya
Cari soal Matematika, Fisika, Kimia dan tonton video pembahasan biar ngerti materinya.
Matematika adalah alat yang hebat yang membantu kita mengungkap dunia yang kita tinggali. Dalam proyek ini, kita akan membahas konsep yang disebut "Jumlah Koefisien Binomial", yang mungkin terlihat kompleks pada awalnya, tetapi akan meresap dalam banyak aspek dari studi Matematika kita. Konsep ini didasarkan pada teorema Newton yang terkenal, yang merupakan ekspansi dari binomial (a+b)^n. Binomial Newton bukan hanya trik matematika, tetapi alat yang memungkinkan kita mengerti fenomena alam dan ilmiah.
Teorema binomial, atau binomial Newton, adalah rumus yang memberikan ekspansi pangkat dari binomial. Teorema ini memiliki aplikasi praktis dalam beragam bidang, termasuk Fisika dan Teknik. Oleh karena itu, memahami jumlah koefisien sangat penting untuk membedakan ekspansi dari binomial. Artinya jumlah koefisien dari binomial akan sama dengan (a+b)^n.
Aplikasi dari teori binomial dan jumlah koefisiennya sangat luas. Misalnya, di bidang Fisika, ekspansi binomial dapat digunakan untuk mendekati nilai dalam beberapa persamaan, sementara di bidang Statistik, ekspansi ini digunakan dalam distribusi binomial. Di Ilmu Komputer, ekspansi binomial dan jumlah koefisien diaplikasikan pada algoritma dan program.
Untuk membantu Anda mendalami topik ini, berikut beberapa sumber terpercaya:
Menentukan Suku dan Koefisien Binomial
$(a+b)^n = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \, \, $
Maka suku ke-$k$ bentuk suku banyak hasil penjabarannya dapat ditentukan dengan rumus : Suku ke-$k \, $ adalah $ \, C_{(k-1)}^n a^{n-(k-1)}b^{k-1} $.
Misalkan ada bentuk $ (2a + 3b)^3 \, $ yang bisa dijabarkan menjadi : $ \begin{align} (2a + 3b)^3 & = 8a^3 + 36a^2b + 54ab^2 + 27b^3 \end{align} $ Suku-suku dari ekspansi binomial $ (2a + 3b)^3 \, $ adalah : Suku ke-1 : $ \begin{align} 8a^3 \end{align} \, $ dengan koefisiennya 8. Suku ke-2 : $ \begin{align} 36a^2b \end{align} \, $ dengan koefisiennya 36. Suku ke-3 : $ \begin{align} 54ab^2 \end{align} \, $ dengan koefisiennya 54. Suku ke-4 : $ \begin{align} 27b^3 \end{align} \, $ dengan koefisiennya 27. Tentu kita tidak perlu menjabarkan sejara keseluruhan suku-sukunya jika hanya menentukan suku tertentu saja. Misalkan kita ingin mencari suku ke-2 dari bentuk binomial $ (2a + 3b)^3 \, $ , maka kita peroleh : Suku ke-2 dengan $ k = 2 $ : $ \begin{align} C_{(k-1)}^n x^{n-(k-1)}y^{k-1} & = C_{(2-1)}^3 (2a)^{3-(2-1)}(3b)^{2-1} \\ & = C_{1}^3 (2a)^{2}(3b)^{1} \\ & = 3. 4.a^2 .3b = 36a^2b \end{align} $. artinya suke ke-2 dari binomial $ (2a + 3b)^3 \, $ adalah $ 36a^2b \, $ yang sesuai dengan bentuk di atasnya.
Contoh soal koefisien binomial : 2). Tentukan suku ke-3 dari binomial $ (2x – 5y)^{20} \, $ dan besar koefisiennya. Penyelesaian : *). Bentuk binomialnya : $ (2x – 5y)^{20} \, $ artinya $ n = 20 $. *). Yang diminta suku ke-3 artinya $ k = 3 $. Rumus suku ke-$k \, $ adalah $ \, C_{(k-1)}^n a^{n-(k-1)}b^{k-1} $ . Suku ke-2 yaitu dari $ (2x – 5y)^{20} = (2x + (- 5y))^{20} \, $ : $ \begin{align} C_{(k-1)}^n a^{n-(k-1)}b^{k-1} & = C_{(3-1)}^{20} (2x)^{20-(3-1)}(-5y)^{3-1} \\ & = C_{2}^{20} (2x)^{18}(-5y)^{2} \\ & = \frac{20!}{(20-2)!2!} . 2^{18}.x^{18}(-5)^2.y^{2} \\ & = \frac{20!}{18!2!} . 2^{18}.x^{18}.25.y^{2} \\ & = \frac{20.19.18!}{18!.2.1} . 2^{18}.x^{18}.25.y^{2} \\ & = \frac{20.19}{2} . 2^{18}.x^{18}.25.y^{2} \\ & = 190 . 2^{18}.x^{18}.25.y^{2} \\ & = (190 \times 2^{18} \times 25). x^{18}y^{2} \\ & = 4750 \times 2^{18} x^{18}y^{2} \end{align} $. Sehingga suku ke-3 dari $ (2x – 5y)^{20} \, $ adalah $ \, 4750 \times 2^{18} x^{18}y^{2} \, $ dengan koefisiennya adalah $ 4750 \times 2^{18} $.
Untuk soal nomor 3 dan nomor 4 berikut gunakan beberapa sifat eksponen : $ \frac{1}{a^n} = a^{-n} \, $ dan $ \, a^m . a^n = a^{m+n} $
3). Diketahi bentuk binomial $ (3a + b)^{50} \, $. Tentukan koefisien dari suku yang berbentuk $ a^{26}b^{24} \, $ dan terletak pada suku ke berapakah suku tersebut. Penyelesaian : *). Bentuk $ (3a + b)^{50} \, $ , artinya $ n = 50 $. *). Rumus suku ke-$k $ adalah $ C_{(k-1)}^n a^{n-(k-1)}b^{k-1} \, $ sehingga sama dengan $ a^{26}b^{24} $. $ \begin{align} a^{n-(k-1)}b^{k-1} & = a^{26}b^{24} \\ a^{50-(k-1)}b^{k-1} & = a^{26}b^{24} \\ a^{50-(k-1)}b^{k-1} & = a^{26}b^{24} \end{align} $. Dari persamaan terakhir di atas diperoleh : $ k – 1 = 24 \rightarrow k = 25 $. Artinya bentuk $ a^{26}b^{24} \, $ adalah suku ke-25. *). Menentukan koefisien suku ke-25 dengan $ k = 25 $ dari bentuk $ (3a + b)^{50} \, $ $ \begin{align} C_{(k-1)}^n x^{n-(k-1)}x^{k-1} & = C_{(25-1)}^{50} (3a)^{50-(25-1)}(b)^{25-1} \\ & = C_{24}^{50} (3a)^{26}(b)^{24} \\ & = C_{24}^{50} 3^{26}a^{26}b^{24} \end{align} $. Jadi, koefisien dari bentuk $ a^{26}b^{24} \, $ adalah $ C_{24}^{50} \times 3^{26} $.
4). Diketahui bentuk binomial $ \left( x – \frac{1}{x} \right)^{2016} \, $ . Tentukan suku yang memuat bentuk $ x^{16} \, $ dan besar koefisiennya. Penyelesaian : *). Bentuk $ \left( x – \frac{1}{x} \right)^{2016} \, $ , artinya $ n = 2016 $. *). Rumus suku ke-$k $ adalah $ C_{(k-1)}^n a^{n-(k-1)}b^{k-1} \, $ sehingga sama dengan $ x^{16} $. Bentuk $ \left( x – \frac{1}{x} \right)^{2016} = \left( x + (- \frac{1}{x} ) \right)^{2016} \, $ artinya $ a = x \, $ dan $ b = – \frac{1}{x} = -x^{-1} $. $ \begin{align} a^{n-(k-1)}b^{k-1} & = x^{16} \\ x^{2016-(k-1)}\left( -x^{-1} \right)^{k-1} & = x^{16} \\ x^{2017-k} . (-1)^{k-1} . \left( x^{-1} \right)^{k-1} & = x^{16} \\ (-1)^{k-1} . x^{2017-k} . \left( x \right)^{1-k} & = x^{16} \\ (-1)^{k-1} . x^{(2017-k)+(1-k)} & = x^{16} \\ (-1)^{k-1} . x^{2018 – 2k} & = x^{16} \\ \end{align} $. Dari persamaan terakhir di atas diperoleh : $ 2018 – 2k = 16 \rightarrow k = 1001 $. Artinya bentuk $ x^{16} \, $ adalah suku ke-1001. *). Menentukan koefisien suku ke-1001 dengan $ k = 1001 $ dari bentuk $ \left( x – \frac{1}{x} \right)^{2016} \, $ $ \begin{align} C_{(k-1)}^n a^{n-(k-1)}b^{k-1} & = C_{(1001-1)}^{2016} (x)^{2016-(1001-1)}(-x^{-1})^{1001-1} \\ & = C_{1000}^{2016} (x)^{1016}(-x^{-1})^{1000} \\ & = C_{1000}^{2016} (x)^{1016}(x^{-1})^{1000} \\ & = C_{1000}^{2016} (x)^{1016}(x)^{-1000} \\ & = C_{1000}^{2016} (x)^{1016 + (-1000)} \\ & = C_{1000}^{2016} x^{16} \end{align} $. Jadi, koefisien dari bentuk $ x^{16} \, $ adalah $ C_{1000}^{2016} $.
Kombinatorika - Ekspansi Binomial
Judul Aktivitas: "Mengupas Ekspansi Binomial"
Mendapatkan pemahaman yang kuat tentang ekspansi binomial Newton dan jumlah dari koefisiennya, dengan mempraktikkan penyelesaian soal tentang topik tersebut dan berdiskusi secara kelompok. Tujuan utama proyek ini adalah untuk belajar menghitung soal binomial yang melibatkan jumlah koefisien dari ekspansi binomial.
Poem by Shane Dizzy Sukardy
Begitulah takdir persahabatan. Ketika habis kelak ucapan dan obrolan, sesegera mulut mewanti-wanti seonggok alasan, agar dapat melanggar garis pertemuan.
Misalkan $S = (x-1)^4 + 4(x-1)^3$ $+ 6(x-1)^2 + 4(x-1) + 1.$ Jika disederhanakan, maka $S = \cdots \cdot$ A. $(x-2)^4$ D. $(x+1)^4$ B. $(x-1)^4$ E. $x^4+1$ C. $x^4$
Berdasarkan teorema binomial, diketahui bahwa $(a+b)^4$ dapat dijabarkan menjadi $a^4+4a^3b + 6a^2b^2 + 4ab^3 + b^4.$ Bentuk $S$ akan sama dengan penjabaran tersebut jika kita mengambil nilai $a = x-1$ dan $b = 1.$ Oleh karena itu, dapat kita tuliskan $$\begin{aligned} S & = (x-1)^4 + 4(x-1)^3 + 6(x-1)^2 + 4(x-1) + 1 \\ & = ((x-1) + 1)^4 \\ & = x^4. \end{aligned}$$Jadi, bentuk sederhana dari $S$ adalah $\boxed{x^4}$ (Jawaban C)
Jika disusun dimulai dari suku dengan variabel berpangkat tertinggi, maka suku keenam setelah $\left(2x^{1/2}-\dfrac14x^{1/4}\right)^9$ diekspansi adalah $\cdots \cdot$ A. $-\dfrac{63}{32}x^{13/4}$ D. $\dfrac{31}{16}x^{9/4}$ B. $\dfrac{63}{32}x^{13/4}$ E. $-\dfrac{15}{8}x^{5/4}$ C. $-\dfrac{31}{16}x^{9/4}$
Suku keenam dari hasil ekspansi binomial tersebut dinyatakan oleh $$\begin{aligned} \text{U}_6 & = C_5^9(2x^{1/2})^{9-5}\left(-\dfrac14x^{1/4}\right)^5 \\ & = \dfrac{9!}{5! \cdot 4!}(2x^{1/2})^4\left(-\dfrac14x^{1/4}\right)^5 \\ & = \dfrac{9 \cdot \cancelto{2}{8} \cdot 7 \cdot \bcancel{6} \cdot \bcancel{5!}}{\bcancel{5!} \cdot \cancel{4} \cdot \bcancel{3 \cdot 2}}(2)^4(x^{1/2})^4 \left(-\dfrac14\right)^5(x^{1/4})^5 \\ & = -(\color{blue}{9} \cdot 2 \cdot \color{blue}{7})(2)^4(2)^{-10}x^2(x^{5/4}) \\ & = -\color{blue}{63}(2^{1+4-10})x^{2 + 5/4} \\ & = -\dfrac{63}{32}x^{13/4}. \end{aligned}$$Jadi, suku keenam dari hasil ekspansi binomial tersebut adalah $\boxed{-\dfrac{63}{32}x^{13/4}}$ (Jawaban A)
Baca Juga: Soal dan Pembahasan – Faktorial
Banyaknya suku yang mengandung ekspresi $x^7$ dari ekspansi $(3x^2-2y^3)^8$ adalah $\cdots \cdot$ A. $0$ C. $2$ E. $4$ B. $1$ D. $3$
Perhatikan bahwa suku $3x^2$ akan selalu berpangkat genap pada variabel $x$ bila dipangkatkan bilangan bulat dari $0$ sampai $8$. Ini menunjukkan bahwa tidak ada satu pun kombinasi perkalian dua suku yang menghasilkan ekspresi $x^7$ karena pangkatnya ganjil. Jadi, tidak ada suku yang mengandung ekspresi $x^7$ dari ekspansi binomial tersebut sehingga koefisien $x^7$ sama dengan $\boxed{0}$ (Jawaban A)
Koefisien suku yang mengandung $x^{14}$ dari ekspansi $(x+2x^3)^{10}$ adalah $\cdots \cdot$ A. $40$ C. $120$ E. $360$ B. $90$ D. $180$
Kombinasi perkalian suku yang mungkin untuk $x^{14}$ adalah $(x)^p(x^3)^q = x^{14}$ dengan $\color{red}{p + q = 10}$. Persamaan eksponen $(x)^p(x^3)^q = x^{14}$ mengimplikasikan bahwa $\color{red}{p + 3q = 14}.$ Selesaikan dan kita akan memperoleh $p = 8$ dan $q = 2.$ Karena $q = 2,$ suku yang dimaksud merupakan suku ke-$2+1 = 3.$ Dalam hal ini, kita memilih $q$ (dan bukan $p)$ karena $q$ merupakan eksponen $b$ dari bentuk $(a+b)^n$ yang langsung menunjukkan suku mana penjabaran itu didapat. $$\begin{aligned} \text{Suku ke-}3 & = C_2^{10} x^8(2x^3)^2 \\ & = \dfrac{10!}{8! \cdot 2!} x^8(4x^6) \\ & = \dfrac{10 \cdot 9 \cdot \cancel{8!}}{\cancel{8!} \cdot 2} (4x^{14}) \\ & = 45(4x^{14}) = 180x^{14} \end{aligned}$$Jadi, koefisien suku yang mengandung $x^{14}$ adalah $\boxed{180}$ (Jawaban D)
Koefisien suku yang mengandung $x^{4}$ dari ekspansi $\left(\dfrac{2}{x}+\dfrac{x^2}{4}\right)^{14}$ adalah $\cdots \cdot$ A. $\dfrac{3003}{2}$ D. $\dfrac{3003}{16}$ B. $\dfrac{3003}{4}$ E. $\dfrac{1551}{16}$ C. $\dfrac{3003}{8}$
Ekspresi $x^4$ terbentuk dari kombinasi perkalian suku $\dfrac{1}{x}=x^{-1}$ dan $x^2$. Kombinasi yang mungkin untuk menghasilkan $x^4$ adalah $(x^{-1})^p(x^2)^q = x^4$ dengan $\color{red}{p + q = 14}.$ Perhatikan bahwa $(x^{-1})^p(x^2)^q = x^4$, yang artinya $\color{red}{-p + 2q = 4}$. Selesaikan dan kita akan memperoleh $p = 8$ dan $q = 6.$ Karena $q = 6$, kita akan mencari suku ke-$6+1=7.$ $$\begin{aligned} \text{Suku ke-}7 & = C_6^{14} \left(\dfrac{2}{x}\right)^8\left(\dfrac{x^2}{4}\right)^6 \\ & = \dfrac{14!}{8! \cdot 6!} (2)^8(x^{-1})^8(x^2)^6(4^{-1})^6 \\ & = \dfrac{14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9 \cdot \cancel{8!}}{\cancel{8!} \cdot 6!}(2^8)(x^{-8})(x^{12})(2^{-12}) \\ & = \dfrac{14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9}{6!}(2^{-4})x^4 \\ & = \dfrac{3003}{16}x^4 \end{aligned}$$Jadi, koefisien suku yang mengandung $x^4$ adalah $\boxed{\dfrac{3003}{16}}$ (Jawaban D)
Konstanta dari hasil penjabaran $\left(3x^3-\dfrac{2}{x}\right)^8$ adalah $\cdots \cdot$ A. $14.328$ D. $16.128$ B. $15.552$ E. $16.136$ C. $16.112$
Mencari konstanta sama artinya dengan mencari koefisien dari $x^0.$ Ekspresi $x^0$ terbentuk dari kombinasi perkalian suku $x^3$ dan $\dfrac{1}{x} = x^{-1}.$ Kombinasi yang mungkin untuk menghasilkan $x^0$ adalah $(x^3)^p(x^{-1})^q = x^0$, dan dari sini kita peroleh SPLDV berikut. $$\begin{cases} p + q & = 8 && (\text{jumlah pangkat dari binomial}) \\ 3p-q & = 0 && (\text{kesamaan pangkat}) \end{cases}$$Selesaikan dan kita peroleh $p = 2$ dan $q = 6.$ Karena $q = 6$, kita akan mencari koefisien suku ke-$6+1 = 7.$ $$\begin{aligned} \text{Suku ke-7} & = C_6^8 (3x^3)^2\left(-\dfrac{2}{x}\right)^6 \\ & = \dfrac{8!}{6! \cdot 2!}(9\cancel{x^6})\left(\dfrac{64}{\cancel{x^6}}\right) \\ & = \dfrac{8 \times 7}{2} \cdot 9 \cdot 64 = 16.128 \end{aligned}$$Jadi, konstanta dari hasil penjabaran $\left(3x^3-\dfrac{2}{x}\right)^8$ adalah $\boxed{16.128}$ (Jawaban D)
Koefisien $a^2b^3c^6$ dalam ekspansi $(a+b+c)^{11}$ adalah $\cdots \cdot$ A. $3.520$ D. $4.620$ B. $3.880$ E. $5.080$ C. $4.520$
Diberikan trinomial $(a+b+c)^{11}$. Pilih $a$ dari $2$ faktor di antara $11$ faktor yang bisa dilakukan dalam $C_2^{11}$ cara. Pilih $b$ dari $3$ faktor di antara $11-2=9$ faktor yang bisa dilakukan dalam $C_3^{9}$ cara. Pilih $c$ dari $6$ faktor di antara $6$ faktor tersisa yang bisa dilakukan dalam $C_6^{6}$ cara. Dengan demikian, koefisien $a^2b^3c^6$ sama dengan $$\begin{aligned} & C_2^{11} \cdot C_3^9 \cdot C_6^6 \\ & = \dfrac{11!}{9! \cdot 2!} \cdot \dfrac{9!}{6! \cdot 3!} \cdot \dfrac{6!}{0! \cdot 6!} \\ & = \dfrac{11 \cdot 10}{2} \cdot \dfrac{9 \cdot 8 \cdot 7}{3!} \cdot 1 \\ & = 4.620. \end{aligned}$$Jadi, koefisien $a^2b^3c^6$ dalam ekspansi $(a+b+c)^{11}$ adalah $\boxed{4.620}$ (Jawaban D)
Koefisien suku $x^{23}$ dari ekspansi $\left(1+\dfrac{1}{99}x^5+\dfrac{1}{10}x^9\right)^{100}$ adalah $\cdots \cdot$ A. $35$ C. $49$ E. $192$ B. $42$ D. $98$
Kombinasi yang mungkin untuk menghasilkan $x^{23}$ adalah $$(1)^p \left(\dfrac{1}{99}x^5\right)^q \left(\dfrac{1}{10}x^9\right)^r = kx^{23}$$dengan $p + q + r = 100.$ Dalam kasus ini, nilai $p$ dapat ditentukan paling akhir karena $1^p = 1$ dengan $0 \leq p \leq 100.$ Dengan menyamakan pangkatnya, kita peroleh persamaan $5q + 9r = 23$ dengan $q + r \leq 100.$ Persamaan tersebut bisa diselesaikan dengan menggunakan konsep persamaan Diophantine (karena $q, r$ bilangan bulat), tetapi memakan waktu yang lama. Gunakan saja cara coba-coba (try and error) untuk menentukan nilai $q$ dan $r$ yang memenuhi persamaan tersebut. Kita akan memperoleh $q = 1$ dan $r = 2$ sehingga $p = 97$. Suku yang mengandung $x^{23}$ adalah $$\begin{aligned} & C_1^{100} \cdot C_2^{99} \cdot C_{97}^{97} \left(\dfrac{1}{99}x^5\right)^1\left(\dfrac{1}{10}x^9\right)^2 \cdot 1^{97} \\ & = \dfrac{100!}{99! \cdot 1!} \cdot \dfrac{99!}{97! \cdot 2!} \cdot 1 \left(\dfrac{1}{99}\right)\left(\dfrac{1}{100}\right)x^5 \cdot x^{18} \\ & = \cancel{100} \cdot \dfrac{\bcancel{99} \cdot 98}{2} \cdot \dfrac{1}{\bcancel{99}} \cdot \dfrac{1}{\cancel{100}} x^{23} = 49x^{23}. \end{aligned}$$Jadi, koefisien $x^{23}$ dari ekspansi trinomial tersebut adalah $\boxed{49}$ (Jawaban C)
Baca Juga: Materi, Soal, dan Pembahasan – Pembuktian Kombinatorial
Nilai dari $C_0^{2.020} + C_1^{2.020} + C_2^{2.020} +$ $\cdots + C_{2.020}^{2.020}$ adalah $\cdots \cdot$ A. $2.020$ D. $2^{2.020}$ B. $2^{1.010}$ E. $10^{2.020}$ C. $2^{2.019}$
Berdasarkan teorema binomial, kita tahu bahwa $(a+b)^n = C_0^n a^n + C_1^n a^{n-1}b +$ $C_2^n a^{n-2}b^2 + \cdots + C_n^n b^n.$ Misalkan $a = b = 1.$ Kita akan memperoleh $$\begin{aligned} (1+1)^n & = C_0^n 1^n + C_1^n 1^{n-1} \cdot 1 + C_2^n 1^{n-2} \cdot 1^2 + \cdots + C_n^n 1^n \\ 2^n & = C_0^n + C_1^n + C_2^n + \cdots + C_n^n. \end{aligned}$$Untuk $n = 2.020,$ didapat $2^{2020} = C_0^{2.020} + C_1^{2.020} + C_2^{2.020} +$ $\cdots + C_{2.020}^{2.020}.$ (Jawaban D)
Jika $A$ menyatakan banyak suku dari ekspansi $(a+b+c+d)^6$ dan $B$ menyatakan banyak suku dari ekspansi $(a+b+c+d+e)^7$, maka selisih $A$ dan $B$ adalah $\cdots \cdot$ A. $12$ C. $15$ E. $20$ B. $14$ D. $16$
Banyaknya suku dari ekspansi multinomial $(a_1+a_2+a_3+\cdots+a_u)^n$ adalah $C_{u-1}^{n+u-1}$ dengan $n$ adalah pangkat dan $u$ adalah banyak sukunya. Untuk itu, multinomial $(a+b+c+d)^6$ memiliki nilai $n = 6$ dan $u = 4$ sehingga $A = C_{4-1}^{6+4-1} = C_3^9 = \dfrac{9!}{6! \cdot 3!} = 84.$ Multinomial $(a+b+c+d+e)^4$ memiliki nilai $n=4$ dan $u=5$ sehingga $B = C_{5-1}^{4+5-1} = C_4^8 = \dfrac{8!}{4! \cdot 4!} = 70.$ Dengan demikian, $A-B = 84-70=14.$ Jadi, selisih nilai $A$ dan $B$ adalah $\boxed{14}$ (Jawaban B)
Diketahui suku kedua dan suku ketiga dari penjabaran $\left(1+\dfrac14\right)^n$ nilainya sama. Nilai $n$ adalah $\cdots \cdot$ A. $5$ C. $8$ E. $11$ B. $6$ D. $9$
Pada penjabaran $\left(1+\dfrac14\right)^n$ dengan $n > 0$, diperoleh $\begin{aligned} \text{Suku kedua} & = \displaystyle \binom{n}{1}(1)^{n-1} \cdot \left(\dfrac14\right)^1 \\ & = n(1)\left(\dfrac14\right) = \dfrac{n}{4} \end{aligned}$ dan $\begin{aligned} \text{Suku ketiga} & = \displaystyle \binom{n}{2}(1)^{n-2} \cdot \left(\dfrac14\right)^2 \\ & = \dfrac{n!}{(n-2)! \cdot 2!}(1) \cdot \dfrac{1}{16} \\ & = \dfrac{n(n-1)}{32}. \end{aligned}$ Karena suku kedua sama dengan suku ketiga, kita dapatkan $\begin{aligned} \dfrac{\bcancel{n}}{\cancel{4}} & = \dfrac{\bcancel{n}(n-1)}{\cancelto{8}{32}} \\ 1 & = \dfrac{n-1}{8} \\ n-1 & = 8 \\ n & = 9. \end{aligned}$ Jadi, nilai $n$ adalah $\boxed{9}$ (Jawaban D)
Jumlah koefisien dari $(8x-7y)^{100} + (5x-6y)^{100}$ adalah $\cdots \cdot$ A. $-1$ C. $1$ E. $3$ B. $0$ D. $2$
Substitusi $x = y = 1$ pada penjumlahan dua binomial $(8x-7y)^{100} + (5x-6y)^{100}$ akan menghasilkan jumlah koefisien tiap suku-suku penjabarannya. $$\begin{aligned} \text{S} & = (8(1)-7(1))^{100} + (5(1)-6(1))^{100} \\ & = 1^{100} + (-1)^{100} \\ & = 1+1=2 \end{aligned}$$Jadi, jumlah koefisien dari $(8x-7y)^{100} + (5x-6y)^{100}$ adalah $\boxed{2}$ (Jawaban D)
Nilai dari $\displaystyle \sum_{k=1}^{2.007} \binom{2.008}{k}2.008^k$ adalah $\cdots \cdot$ A. $2.008^{2.008}-2.007^{2.008}-1$ B. $2.008^{2.008}-2.008^{2.008}-1$ C. $2.009^{2.008}-2.008^{2.008}-1$ D. $2.009^{2.007}-2.008^{2.007}-1$ E. $2.009^{2.009}-2.008^{2.008}-1$
Perhatikan bahwa dengan menggunakan teorema binomial, kita peroleh $$\begin{aligned} (2.008+1)^{2.008} & = \displaystyle \sum_{k = 0}^{2.008} \binom{2.008}{k}2.008^k(1)^{2.008-k} \\ 2.009^{2.008}& = \sum_{k=0}^{2.008} \binom{2.008}{k} 2.008^k \\ & = \binom{2.008}{0} 2.008^0 + \sum_{k=1}^{2.007} 2.008^k + \binom{2.008}{2.008} 2.008^{2.008} \\ & = 1 + \sum_{k=1}^{2.007} 2.008^k + 2.008^{2.008}. \end{aligned}$$Dari persamaan terakhir di atas, diperoleh $\boxed{\displaystyle \sum_{k=1}^{2.007} 2.008^k = 2.009^{2.008}-2.008^{2.008}-1}$ (Jawaban C)
Ekspansikan (jabarkan) ekspresi aljabar berikut. a. $(a+b)^6$ b. $(3x+y)^9$ c. $(x-2y)^5$
Gunakan teorema binomial. Jawaban a) $$\begin{aligned} (a+b)^6 & = C_0^6 a^6 + C_1^6 a^5b + C_2^6 a^4b^2 + C_3^6 a^3b^3 + C_4^6 a^2b^4 + C_5^6 ab^5 + C_6^6 b^6 \\ & = \dfrac{6!}{6! \cdot 0!} a^6 + \dfrac{6!}{5! \cdot 1!} a^5b + \dfrac{6!}{4! \cdot 2!} a^4b^2 + \dfrac{6!}{3! \cdot 3!} a^3b^3 + \dfrac{6!}{2! \cdot 4!} a^2b^4 + \dfrac{6!}{1! \cdot 5!} ab^5 + \dfrac{6!}{0! \cdot 6!} b^6 \\ & = a^6 + 6a^5b + 15a^4b^2 + 20a^3b^3 + 15a^2b^4 + 6ab^5 + b^6 \end{aligned}$$Jawaban b) $$\begin{aligned} (3x+y)^9 & = C_0^9 (3x)^9 + C_1^9 (3x)^8y + C_2^9 (3x)^7y^2 + C_3^9 (3x)^6y^3 + C_4^9 (3x)^5y^4 + C_5^9 (3x)^4y^5 + C_6^9 (3x)^3y^6 + C_7^9 (3x)^2y^7 + C_8^9 (3x)y^8 + C_9^9 y^9 \\ & = \dfrac{9!}{9! \cdot 0!} 19683x^9 + \dfrac{9!}{8! \cdot 1!} 6561x^8y + \dfrac{9!}{7! \cdot 2!} 2187x^7y^2 + \dfrac{9!}{6! \cdot 3!} 729x^6y^3 + \dfrac{9!}{5! \cdot 4!} 243x^5y^4 + \dfrac{9!}{4! \cdot 5!} 81x^4y^5 + \dfrac{9!}{3! \cdot 6!} 27x^3y^6 + \dfrac{9!}{2! \cdot 7!} 9x^2y^7 + \dfrac{9!}{1! \cdot 8!} 3xy^8 + \dfrac{9!}{0! \cdot 9!} y^9 \\ & = (1)19.683x^9 + (9)6.561x^8y + (36)2.187x^7y^2 + (84) 729x^6y^3 + (126)243x^5y^4 + (126)81x^4y^5 + (84) 27x^3y^6 + (36)9x^2y^7 + (9)3xy^8 + (1)y^9 \\ & = 19.683x^9 + 59.049x^8y + 78.732x^7y^2 + 61.236x^6y^3 + 30.618x^5y^4 + 10.206x^4y^5 + 2.268x^3y^6 + 324x^2y^7 + 27xy^8 + y^9 \end{aligned}$$Jawaban c) $$\begin{aligned} (x-2y)^5 & = C_0^5 x^5 + C_1^5 x^4(-2y) + C_2^5 x^3(-2y)^2 + C_3^5 x^2(-2y)^3 + C_4^5 x(-2y)^4 + C_5^5 (-2y)^5 \\ & = \dfrac{5!}{0! \cdot 5!} x^5 + \dfrac{5!}{1! \cdot 4!} (-2x^4y) + \dfrac{5!}{2! \cdot 3!} (4x^3y^2) + \dfrac{5!}{3! \cdot 2!} (-8x^2y^3) + \dfrac{5!}{4! \cdot 1!} (16xy^4) + \dfrac{5!}{5! \cdot 0!} (-32y^5) \\ & = 1x^5 + 5(-2x^4y) + 10(4x^3y^2) + 10(-8x^2y^3) + 5(16xy^4) + 1(-32y^5) \\ & = x^5-10x^4y+40x^3y^2-80x^2y^3 +80xy^4-32y^5 \end{aligned}$$
Hitunglah: a. $(\sqrt3+1)^5-(\sqrt3-1)^5$ b. $(2+\sqrt5)^5+(2-\sqrt5)^5$
Jawaban a) Jabarkan $(\sqrt3+1)^5$ menggunakan teorema binomial. $$\begin{aligned} (\sqrt3+1)^5 & = C_0^5 (\sqrt3)^5 + C_1^5 (\sqrt3)^4(1) + C_2^5 (\sqrt3)^3(1)^2 + C_3^5 (\sqrt3)^2(1)^3 + C_4^5 (\sqrt3)(1)^4 + C_5^5 (1)^5 \\ & = 9\sqrt3 + 5(9)(1) + 10(3\sqrt3)(1) + 10(3)(1) + 5(\sqrt3)(1) + 1 \\ & = 9\sqrt3 + 45 + 30\sqrt3 + 30 + 5\sqrt3 + 1 \\ & = 44\sqrt3 + 76 \end{aligned}$$Dengan cara yang serupa, kita peroleh $$\begin{aligned} (\sqrt3-1)^5 & = 9\sqrt3 -5(9)(1) + 10(3\sqrt3)(1)- 10(3)(1) + 5(\sqrt3)(1)-1 \\ & = 9\sqrt3 -45 + 30\sqrt3- 30 + 5\sqrt3 -1 \\ & = 44\sqrt3-76. \end{aligned}$$Dengan demikian, didapat $\begin{aligned} & (\sqrt3+1)^5-(\sqrt3-1)^5 \\ & = (44\sqrt3+76)-(44\sqrt3-76) \\ & = 76+76 = 152. \end{aligned}$ Jadi, hasil dari $(\sqrt3+1)^5-(\sqrt3-1)^5$ adalah $\boxed{152}$ Jawaban b) Jabarkan $(2+\sqrt5)^5+(2-\sqrt5)^5$ menggunakan teorema binomial. $$\begin{aligned} (2+\sqrt5)^5 & = C_0^5 (2)^5 + C_1^5 (2)^4(\sqrt5) + C_2^5 (2)^3(\sqrt5)^2 + C_3^5 (2)^2(\sqrt5)^3 + C_4^5 (2)(\sqrt5)^4 + C_5^5 (\sqrt5)^5 \\ & = 1(32) + 5(16)(\sqrt5) + 10(8)(5) + 10(4)(5\sqrt5) + 5(2)(25) + 1(25\sqrt5) \\ & = 32 + 80\sqrt5 + 400 + 200\sqrt5 + 250 + 25\sqrt5 \\ & = 305\sqrt5 + 682 \end{aligned}$$Dengan cara yang serupa, kita peroleh $$\begin{aligned} (2-\sqrt5)^5 & = 1(32) -5(16)(\sqrt5) + 10(8)(5)- 10(4)(5\sqrt5) + 5(2)(25)- 1(25\sqrt5) \\ & = 32 -80\sqrt5 + 400 -200\sqrt5 + 250 -25\sqrt5 \\ & = -305\sqrt5 + 682. \end{aligned}$$Dengan demikian, didapat $\begin{aligned} & (2+\sqrt5)^5+(2-\sqrt5)^5 \\ & = (305\sqrt5+682)+(-305\sqrt5+682) \\ & = 682+682 = 1.364. \end{aligned}$ Jadi, hasil dari $(2+\sqrt5)^5+(2-\sqrt5)^5$ adalah $\boxed{1.364}$
Pada penjabaran $(2x-y)^{11}$, tentukan: a. suku ketujuh; b. koefisien suku kelima; c. jumlah semua koefisien penjabarannya.
Jawaban a) Koefisien suku ke-$a$ dari binomial $(x + y)^n$ adalah $\displaystyle \binom{n}{a-1} x^{n-a+1} \cdot y^{a-1}.$ Diketahui $(2x-y)^{11}$ yang berarti $n = 11$ dan kita akan mencari suku ketujuh $(a = 7)$. $$\begin{aligned} \text{Suku ketujuh} & = \displaystyle \binom{n}{a-1} (2x)^{n-a+1} \cdot (-y)^{a-1} \\ & = \binom{11}{7-1} (2x)^{11-7+1}(-y)^{7-1} \\ & = \binom{11}{6} (2x)^5(-y)^6 \\ & = \dfrac{11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot \cancel{5!}}{6! \cdot \cancel{5!}} (32x^5)(y^6) \\ & = 462(32x^5)(y^6) = 14.784x^5y^6 \end{aligned}$$Jadi, suku ketujuhnya adalah $\boxed{14.784x^5y^6}$ Jawaban b) Koefisien suku ke-$k$ dari penjabaran binomial $(ax+by)^n$ ditentukan oleh $\displaystyle \binom{n}{k-1}a^{n-k+1}b^{k-1}$. Untuk itu, koefisien suku ke-$5$ dari penjabaran binomial $(ax+by)^n$ dinyatakan oleh $$\begin{aligned} \text{U}_5 & = \displaystyle \binom{11}{5-1}(2)^{11-5+1}(-1)^{5-1} \\ & = \binom{11}{4}(2)^7(-1)^4 \\ & = \dfrac{11!}{4! \cdot 7!}(2)^7 \\ & = \dfrac{11 \cdot 10 \cdot 9 \cdot 8 \cdot \cancel{7!}}{4! \cdot \cancel{7!}}(2)^7 \\ & = 42.240 \end{aligned}$$Jadi, koefisien suku kelima adalah $\boxed{42.240}$ Jawaban c) Jumlah semua koefisien penjabarannya adalah $(2x-y)^{11}$ ketika $x=y=1$. Kita peroleh, $(2(1)-1)^{11} = 1^{11} = 1$.
Diketahui binomial $(5+2x)^n$ dengan $n$ merupakan bilangan asli. Tentukan nilai $n$ agar koefisien $x^2$ sama dengan dua kali koefisien $x$.
Diketahui binomial $(5+2x)^n.$ Suku yang memuat ekspresi $x^2$ dinyatakan oleh $C_q^n (5)^p(2x)^q = kx^2$ untuk suatu bilangan real $k.$ Persamaan di atas menunjukkan bahwa $q = 2$ sehingga $p = n-2$. Koefisien $x^2$ adalah $C_2^n (5)^{n-2}(2)^2$. Suku yang memuat ekspresi $x$ dinyatakan oleh $C_q^n (5)^p(2x)^q = kx$ untuk suatu bilangan real $k.$ Persamaan di atas menunjukkan bahwa $q = 1$ sehingga $p = n-1.$ Koefisien $x$ adalah $C_1^n (5)^{n-1}(2).$ Koefisien $x^2$ harus sama dengan dua kali koefisien $x$ sehingga $$\begin{aligned} C_2^n (5)^{n-2}(2)^2 & = 2\left(C_1^n (5)^{n-1}(2)\right) \\ \dfrac{n!}{(n-2)! \cdot 2!} (5)^{n-2} (\cancel{4}) & = \cancel{2} \cdot \dfrac{n!}{(n-1)! \cdot 1!} (5)^{n-1} (\cancel{2}) \\ \dfrac{n!}{(n-2)! \cdot 2} \cdot \dfrac{(n-1)!}{(n)!} & = \dfrac{5^{n-1}}{5^{n-2}} \\ \dfrac{n-1}{2} & = 5 \\ n-1 & = 10 \\ n & = 11. \end{aligned}$$Jadi, nilai $n$ agar $\boxed{11}$
Jika $n>0$ merupakan koefisien $x$ pada bentuk binomial $(nx-y)^6$ dan diketahui bahwa rasio koefisien suku ketiga dan kelima setelah binomialnya dijabarkan adalah $4 : 1$, tentukan nilai $n.$
Diketahui binomial $(nx-y)^6.$ Suku ketiga hasil ekspansi binomial tersebut adalah $\begin{aligned} \text{U}_3 & = C_2^6 (nx)^4(-y)^2 \\ & = \dfrac{6!}{4! \cdot 2!} (n^4x^4)(y^2) \\ & = 15n^4x^4y^2. \end{aligned}$ Koefisien suku ketiga adalah $15n^4.$ Suku kelima hasil ekspansi binomial tersebut adalah $\begin{aligned} \text{U}_5 & = C_4^6 (nx)^2(-y)^4 \\ & = \dfrac{6!}{2! \cdot 4!} (n^2x^2)(y^4) \\ & = 15n^2x^2y^4. \end{aligned}$ Koefisien suku kelima adalah $15n^2.$ Karena rasio (perbandingan) koefisien suku ketiga dan kelima setelah binomialnya dijabarkan adalah $4 : 1$, diperoleh $\begin{aligned} \dfrac{15n^4}{15n^2} & = \dfrac41 \\ n^2 & = 4 \\ n & = \pm 2. \end{aligned}$ Karena diketahui $n > 0$, nilai $n$ yang dimaksud adalah $\boxed{n=2}$
Tunjukkan bahwa rasio koefisien $x^{10}$ pada penjabaran $(1-x^2)^{10}$ dan koefisien $x^0$ pada penjabaran $\left(x-\dfrac{2}{x}\right)^{10}$ adalah $1 : 32.$
Suku yang mengandung ekspresi $x^{10}$ pada penjabaran $(1-x^2)^{10}$ adalah $C_q^{10} (1)^p(-x^2)^q = kx^{10}$ dengan $p + q = 10$. Persamaan di atas mengimplikasikan bahwa $2q = 10$ sehingga $q = 5$, dan akibatnya $p = 5.$ Dengan demikian, suku yang mengandung ekspresi $x^{10}$ pada penjabaran $(1-x^2)^{10}$ adalah $$\begin{aligned} C_5^{10} (1)^5(-x^2)^5 & = \dfrac{10!}{5! \cdot 5!} (1)(-x^{10}) \\ & = \dfrac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot \cancel{5!}}{\cancel{5!} \cdot 5!} (-x^{10}) \\ & = -36x^{10}. \end{aligned}$$Suku yang mengandung ekspresi $x^{0}$ pada penjabaran $\left(x-\dfrac{2}{x}\right)^{10}$ adalah $C_q^{10} (x)^p\left(-\dfrac{2}{x}\right)^q = kx^{0}$ atau ditulis menjadi $C_q^{10} (-2x^{p-q}) = kx^0$ dengan $p+q 10$. Persamaan di atas mengimplikasikan bahwa $p-q = 0.$ Dengan menyelesaikan kedua persamaan tersebut, kita peroleh $p = q = 5.$ Dengan demikian, suku yang mengandung ekspresi $x^{0}$ pada penjabaran $\left(x-\dfrac{2}{x}\right)^{10}$ adalah $$\begin{aligned} C_5^{10} (x)^5\left(-\dfrac{2}{x}\right)^5 & = \dfrac{10!}{5! \cdot 5!} (x^5)\left(-\dfrac{32}{x^5}\right) \\ & = \dfrac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot \cancel{5!}}{\cancel{5!} \cdot 5!} (-32)x^0 \\ & = -36(32)x^{0}. \end{aligned}$$Dengan demikian, perbandingan koefisien $x^{10}$ dan $x^0$ adalah $\boxed{-36 : (-36)(32) = 1 : 32}$ (Terbukti)
Carilah koefisien $x^5$ pada penjabaran $\left(\dfrac{x}{4}-4\right)^7(2+x)$.
Kita akan mencari koefisien $x^4$ dan $x^5$ pada penjabaran $\left(\dfrac{x}{4}-4\right)^7.$ $\begin{aligned} \text{Koef}\text{isien}~x^4 & = C_3^7 \left(\dfrac{1}{4}\right)^4(-4)^3 \\ & = \dfrac{7!}{4! \cdot 3!} \left(-\dfrac14\right) \\ & = \dfrac{7 \cdot \bcancel{6} \cdot 5 \cdot \cancel{4!}}{\cancel{4!} \cdot \bcancel{6}}\left(-\dfrac14\right) \\ & = -\dfrac{35}{4} \end{aligned}$ $\begin{aligned} \text{Koef}\text{isien}~x^5 & = C_2^7 \left(\dfrac{1}{4}\right)^5(-4)^2 \\ & = \dfrac{7!}{5! \cdot 2!} \left(\dfrac14\right)^3 \\ & = \dfrac{7 \cdot 6 \cdot \cancel{5!}}{\cancel{5!} \cdot 2}\left(\dfrac{1}{64}\right) \\ & = \dfrac{21}{64} \end{aligned}$ Koefisien $x^5$ pada penjabaran $\left(\dfrac{x}{4}-4\right)^7(2+x)$ adalah $$\begin{aligned} & (\text{koefi}\text{sien}~x^5)(2) + (\text{koefi}\text{sien}~x^4)(1) \\ & = \dfrac{22}{64} \cdot 2 + \left(-\dfrac{35}{4}\right)(1) \\ & = \dfrac{21}{32}-\dfrac{35 \cdot 8}{32} = -\dfrac{259}{32}. \end{aligned}$$Jadi, koefisien $x^5$ pada penjabaran $\left(\dfrac{x}{4}-4\right)^7(2+x)$ adalah $\boxed{-\dfrac{259}{32}}$
Baca Juga: Masalah Kombinatorika: Mencari Banyak Rute
Tentukan hubungan $a$ dan $b$ agar koefisien $x^7$ dari penjabaran $\left(ax^2+\dfrac{1}{bx}\right)^{11}$ sama dengan koefisien $x^{-7}$ dari penjabaran $\left(ax-\dfrac{1}{bx^2}\right)^{11}.$
Persamaan dari penjabaran binomial $\left(ax^2+\dfrac{1}{bx}\right)^{11}$ yang menghasilkan $x^7$ adalah $\begin{aligned} C_q^{11} (ax^2)^p \left(\dfrac{1}{bx}\right)^q & = kx^7 \\ C_q^{11} \left(a^p \cdot \dfrac{1}{b^q}\right) (x^{2p-q}) & = kx^7 \end{aligned}$ untuk suatu bilangan real $k$ dan $p + q = 11$. Persamaan di atas juga mengimplikasikan bahwa $2p-q = 7.$ Dengan demikian, kita peroleh $p = 6$ dan $q = 5.$ Koefisien $x^7$ dari penjabaran binomial tersebut adalah $\boxed{\text{Koef.}~x^7 = C_{5}^{11} \left(a^6 \cdot \dfrac{1}{b^5}\right)}$ Persamaan dari penjabaran binomial $\left(ax-\dfrac{1}{bx^2}\right)^{11}$ yang menghasilkan $x^{-7}$ adalah $\begin{aligned} C_q^{11} (ax)^p \left(-\dfrac{1}{bx^2}\right)^q & = kx^{-7} \\ C_q^{11} (a^p)\left(-\dfrac{1}{b}\right)^q (x^{p-2q}) & = kx^{-7} \end{aligned}$ untuk suatu bilangan real $k$ dan $p + q = 11.$ Persamaan di atas juga mengimplikasikan bahwa $p-2q = -7.$ Dengan demikian, kita peroleh $q = 6$ dan $p = 5.$ Koefisien $x^{-7}$ dari penjabaran binomial tersebut adalah $\boxed{\text{Koef.}~x^{-7}= C_{6}^{11} (a^5)\left(-\dfrac{1}{b}\right)^6}$ Samakan koefisien $x^7$ dan koefisien $x^{-7}$ tersebut. $\begin{aligned} C_{5}^{11} \left(a^6 \cdot \dfrac{1}{b^5}\right) & = C_{6}^{11} (a^5)\left(-\dfrac{1}{b}\right)^6 \\ \bcancel{\dfrac{11!}{6! \cdot 5!}} \cdot a^6 \cdot \dfrac{1}{b^5} & = \bcancel{\dfrac{11!}{5! \cdot 6!}} \cdot a^5 \cdot \dfrac{1}{b^6} \\ a & = \dfrac{1}{b} \\ ab & = 1 \end{aligned}$ Jadi, hubungan $a$ dan $b$ diberikan oleh $\boxed{ab=1}$
Jika tiga suku pertama penjabaran $(1+ax)^n$ adalah $1+16x+112x^2$, maka tentukan nilai $a$ dan $n$.
Berdasarkan teorema binomial, tiga suku pertama hasil ekspansi (penjabaran) dari $(1+ax)^n$ dinyatakan sebagai berikut. $$\begin{aligned} C_0^n 1^n + C_1^n 1^{n-1}(ax) + C_2^n 1^{n-2}(ax)^2 & = 1 + 16x + 112x^2 \\ (1)(1) + \dfrac{n!}{(n-1)! \cdot 1!} (1)(ax) + \dfrac{n!}{(n-2)! \cdot 2!} (1)(a^2x^2) & = 1+16x+112x^2 \\ 1 + \dfrac{n \cdot \cancel{(n-1)!}}{\cancel{(n-1)!}} (ax) + \dfrac{n(n-1) \cdot \cancel{(n-2)!}}{\cancel{(n-2)!} \cdot 2} (a^2x^2) & = 1+16x+112x^2 \\ 1 + (an)x + \dfrac{a^2n(n-1)}{2}x^2 & = 1+16x+112x^2 \end{aligned}$$Dengan menyamakan koefisien dari setiap suku yang bersesuaian, kita peroleh $an = 16$ sehingga $$\begin{aligned} \dfrac{a^2n(n-1)}{2} & = 112 \\ a^2n^2-a^2n & = 224 \\ (an)^2-a(an) & = 224 \\ 16^2-a(16) & = 224 \\ 256-16a & = 224 \\ -16a & = -32 \\ a & = 2. \end{aligned}$$Karena $\boxed{a = 2}$ dan $an = 16$, haruslah $\boxed{n = 8}$
Uraikan dengan menggunakan perluasan teorema binomial. a. $(1-x+x^2)^3$ b. $(1+x+x^2)^5$
Jawaban a) $(1-x+x^2)$ merupakan trinomial (karena memuat $3$ suku), tetapi bisa dianggap sebagai binomial $((1-x)+x^2).$ Selanjutnya, kita gunakan teorema binomial. $$\begin{aligned} ((1-x)+x^2)^3 & = C_0^3 (1-x)^3 + C_1^3 (1-x)^2(x^2) + C_2^3 (1-x)(x^2)^2 + C_3^3 (x^2)^3 \\ & = 1(1-3x+3x^2-x^3) + 3(1-2x+x^2)(x^2)+3(1-x)(x^4) + 1(x^6) \\ & = (1-3x+3x^2-x^3)+(3x^2-6x^3+3x^4) + (3x^4-3x^5) + x^6 \\ & = x^6-3x^5+6x^4-7x^3+6x^2-3x+1 \end{aligned}$$Jawaban b) $(1+x+x^2)$ merupakan trinomial (karena memuat $3$ suku), tetapi bisa dianggap sebagai binomial $((1+x)+x^2)^5.$ Selanjutnya, kita gunakan teorema binomial. $$\begin{aligned} ((1+x)+x^2)^5 & = C_0^5 (1+x)^5 + C_1^5 (1+x)^4(x^2) + C_2^5 (1+x)^3(x^2)^2 + C_3^5 (1+x)^2(x^2)^3 + C_4^5 (1+x)(x^2)^4 + C_5^5 (x^2)^5 \\ & = 1(1+5x+10x^2+10x^3+5x^4+x^5)+5(1+4x+6x^2+4x^3+x^4)(x^2) + \\ & 10(1+3x+3x^2+x^3)(x^4) + 10(1+2x+x^2)(x^6) + 5(1+x)(x^8) + 1(x^{10}) \\ & = (1+5x+10x^2+10x^3+5x^4+x^5) + (5x^2 + 20x^3 + 30x^4 + 20x^5 + 5x^6) + \\ & (10x^4 + 30x^5 + 30x^6 + 10x^7) + (10x^6 + 20x^7 + 10x^8) + (5x^8 + 5x^9) + x^{10} \\ & = x^{10} + 5x^9 + 15x^8 + 30x^7 + 45x^6 + 51x^5 + 45x^4 + 30x^3 + 15x^2 + 5x + 1 \end{aligned}$$
Carilah nilai pendekatan dari $\sqrt[4]{15}.$
Misal $\sqrt[4]{15} = (16-1)^{\frac14}.$ Berdasarkan penjabaran binomial, kita tahu bahwa $$\boxed{(x+y)^n = x^n + \dfrac{n}{1} x^{n-1}y + \dfrac{n(n-1)}{1 \cdot 2}x^{n-2} \cdot y^2 + \dfrac{n(n-1)(n-2)}{1 \cdot 2 \cdot 3}x^{n-3}y^3 + \cdots}$$Ini berarti $x = 16$, $y = -1,$ dan $n = \dfrac14.$ Dengan demikian, kita peroleh $$\begin{aligned} (16-1)^{\frac14} & \approx 16^{\frac14} + \dfrac14 (16)^{-\frac34}(-1) + \dfrac{\frac14 \cdot \left(-\frac34\right)}{1 \cdot 2}(16)^{-\frac74}(-1)^2 + \cdots \\ & \approx 2-\dfrac14 \cdot \dfrac18 -\dfrac{3}{32} \cdot \dfrac{1}{128}-\cdots \\ & \approx 2-0,031-0,001-\cdots \\ & \approx 1,968 \approx 1,97. \end{aligned}$$Jadi, nilai pendekatan dari $\sqrt[4]{15}$ adalah $\boxed{1,97}$ (dua angka di belakang koma).
Jika $(x+1)^n$ dijabarkan (pangkat $x$ semakin menurun) dengan $n$ bilangan bulat positif, maka diperoleh ada tiga suku berurutan yang memiliki perbandingan koefisien $2 : 15 : 70.$ Tentukan nilai $n$.
Dengan menggunakan teorema binomial, kita tahu bahwa $$\begin{aligned} (x + 1)^n & = \displaystyle \binom{n}{0} x^n + \binom{n}{1}x^{n-1}(1) + \cdots + \binom{n}{n-1}(x)1^{n-1} + \binom{n}{n} (1)^n \\ & = \binom{n}{0} x^n + \binom{n}{1}x^{n-1} + \cdots + \binom{n}{n-1}(x)+ \binom{n}{n}. \end{aligned}$$Perhatikan bahwa setiap koefisien pada masing-masing suku hanya dipengaruhi oleh koefisien binomialnya. Misalkan tiga suku yang berurutan memiliki koefisien binomial $\displaystyle \binom{n}{a},$ $\displaystyle \binom{n}{a+1},$ dan $\displaystyle \binom{n}{a+1}$ untuk suatu bilangan cacah $a$ sehingga berlaku $$\displaystyle \binom{n}{a} : \binom{n}{a+1} : \binom{n}{a+2} = 2 : 15 : 70.$$Karena $\displaystyle \binom{n}{a} : \binom{n}{a+1} = 2 : 15,$ kita peroleh $$\begin{aligned} \dfrac{n!}{(n-a)! \cdot a!} : \dfrac{n!}{(n-a-1)! \cdot (a+1)!} & = 2 : 15 \\ \dfrac{1}{n-a} : \dfrac{1}{a+1} & = 2 : 15 \\ \dfrac{a+1}{n-a} & = \dfrac{2}{15} \\ 15a+15 & = 2n-2a \\ 17a & = 2n-15. && (\cdots 1) \end{aligned}$$Karena $$\displaystyle \binom{n}{a+1} : \binom{n}{a+2} = 15 : 70 = 3 : 14,$$ kita peroleh $$\begin{aligned} \dfrac{n!}{(n-a-1)! \cdot (a+1)!} : \dfrac{n!}{(n-a-2)! \cdot (a+2)!} & = 3 : 14 \\ \dfrac{1}{n-a-1} : \dfrac{1}{a+2} & = 3 : 14 \\ \dfrac{a+2}{n-a-1} & = \dfrac{3}{14} \\ 14a+28 & = 3n-3a-3 \\ 17a & = 3n-31. && (\cdots 2) \end{aligned}$$Dari persamaan $(1)$ dan $(2)$, diperoleh bahwa $n = 16$ dan $a = 1.$ Jika kita periksa, $\begin{aligned} \displaystyle \binom{16}{1} & = \dfrac{16!}{15! \cdot 1!} = 16 \\ \binom{16}{2} & = \dfrac{16!}{14! \cdot 2!} = 8 \times 15 \\ \binom{16}{3} & = \dfrac{16!}{13! \cdot 3!} = 16 \times 35 \end{aligned}$ dengan perbandingan $$\begin{aligned} \displaystyle \binom{n}{1} : \binom{n}{2} : \binom{n}{3} & = 16 : 8 \times 15 : 16 \times 35 \\ & = 2 : 15 : 70 \end{aligned}$$dan ternyata sesuai. Jadi, nilai $\boxed{n = 16}$
Untuk bilangan cacah $k$, dengan $0 \leq k \leq 14$, didefinisikan $a_k$ adalah koefisien dari suku $x^k$ pada polinomial $x^2(x+1)^3(x+2)^4(x+3)^5.$ Tentukan nilai dari $a_2+a_4+a_6+\cdots+a_{14}.$
Ingat bahwa jumlah semua koefisien dari penjabaran $(ax+by)^n$ adalah $(a+b)^n$, yakni ketika $x = y = 1.$ Pada polinomial $P(x) = x^2(x+1)^3(x+2)^4(x+3)^5,$ variabel $x$ memiliki pangkat tertinggi $2+3+4+5=14.$ Koefisien $a_2 + a_4 + \cdots + a_{14}$ merupakan koefisien pada suku-suku genap. Jika kita substitusi $x = 1$ pada $P(x)$, kita peroleh $\begin{aligned} & 1^2(1+1)^3(1+2)^4(1+3)^5 \\ & = 1(2^3)(3^4)(4^5) \\ & = 2^{13} \cdot 3^4. \end{aligned}$ Bilangan ini mewakili jumlah semua koefisien dari setiap suku hasil penjabaran $P(x)$. Jika kita substitusi $x = -1$ pada $P(x),$ kita peroleh $$(-1)^2(-1+1)^3(-1+2)^4(-1+3)^5 = 0.$$Bilangan ini mewakili jumlah koefisien suku genap dikurang jumlah koefisien suku ganjil pada penjabaran $P(x).$ Karena bernilai $0$, itu artinya jumlah koefisien pada suku genap maupun ganjil adalah sama sehingga $$\boxed{a_2+a_4+\cdots+a_{14} = \dfrac{2^{13} \cdot 3^4}{2} = 2^{12} \cdot 3^4}$$
Tentukan banyak suku-suku berbeda pada penjabaran: a. $(x+2y+z)^{10}$ b. $(a+b+c+d+e+f)^{20}$
Jawaban a) Diketahui multinomial $(x+2y+z)^{10}.$ Dari sini, diketahui $n = 10$ dan $r = 3$ (banyak variabelnya). Banyak suku-suku berbeda dari penjabaran binomial tersebut adalah $\begin{aligned} \text{S} & = \displaystyle \binom{n+r-1}{r-1} \\ & = \binom{10 + 3-1}{3-1} \\ & = \binom{12}{2} \\ & = \dfrac{12!}{10! \cdot 2!} \\ & = \dfrac{12 \cdot 11 \cancel{10!}}{\cancel{10!} \cdot 2} \\ & = 66. \end{aligned}$ Jadi, ada $\boxed{66}$ suku-suku berbeda dari penjabaran $(x+2y+z)^{10}.$ Jawaban b) Diketahui multinomial $(a+b+c+d+e+f)^{20}.$ Dari sini, diketahui $n = 20$ dan $r = 6$ (banyak variabelnya). Banyak suku-suku berbeda dari penjabaran binomial tersebut adalah $\begin{aligned} \text{S} & = \displaystyle \binom{n+r-1}{r-1} \\ & = \binom{20 + 6-1}{6-1} \\ & = \binom{25}{5} \\ & = \dfrac{25!}{20! \cdot 5!} \\ & = \dfrac{25 \cdot 24 \cdot 23 \cdot 22 \cdot 21 \cdot \cancel{20!}}{\cancel{20!} \cdot 5!} \\ & = 53.130. \end{aligned}$ Jadi, ada $\boxed{53.130}$ suku-suku berbeda dari penjabaran $(a+b+c+d+e+f)^{20}.$
Carilah koefisien: a. $x^2y^3z^3$ dari penjabaran $(x+2y+z)^8$; b. $x^2y^3z^5$ dari penjabaran $(x+y-z)^{10}$.
Jawaban a) Diketahui $(x+2y+z)^8.$ $$\begin{aligned} \text{Koef.}~x^2y^2z^3 & = \displaystyle \binom{8}{2, 3, 3} \cdot 1^2 \cdot 2^3 \cdot 1^3 \\ & = \dfrac{8!}{2! \cdot 3! \cdot 3!} \cdot 1 \cdot 8 \cdot 1 \\ & = 4.480 \end{aligned}$$Jadi, koefisien $x^2y^3z^3$ dari penjabaran trinomial tersebut adalah $\boxed{4.480}$ Jawaban b) Diketahui $(x+y-z)^{10}$. $$\begin{aligned} \text{Koef.}~x^2y^3z^5 & = \displaystyle \binom{10}{2, 3, 5} \cdot 1^2 \cdot 1^3 \cdot (-1)^5 \\ & = \dfrac{10!}{2! \cdot 3! \cdot 5!} \cdot 1 \cdot 1 \cdot (-1) \\ & = -2.520 \end{aligned}$$Jadi, koefisien $x^2y^3z^5$ dari penjabaran trinomial tersebut adalah $\boxed{-2.520}$
- Sebelumnya kita telah belajar materi "Kombinasi pada Peluang dan Contohnya" yang merupakan bagian dari
. Ternyata konsep kombinasi bisa dikembangkan pada pembahasan
. Pada artikel kali ini kita akan membahas lebih spesipik tentang
mempelajari tentang cara penjabaran(ekspansi) bentuk pangkat aljabar yang terdiri dari dua suku (
Untuk menjabarkan bentuk pangkat aljabar dua suku bisa menggunakan sigitiga
seperti berikut ini :
tersebut dapat membantu dalam penjabaran pangkat dua suku berikut dimana angka-angka pada segitiga pascal merupakan koefisien dari setiap sukunya:
$ \begin{align} (a+b)^0 & = 1 \\ (a+b)^1 & = a + b \\ (a+b)^2 & = a^2 + 2ab + b^2 \\ (a+b)^3 & = a^3 + 3a^2b + 3ab^2 + b^3 \\ (a+b)^4 & = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + y^4 \\ (a+b)^5 & = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5 \\ (a+b)^n & = ..... \end{align} $
Tetapi ada metode lain yang lebih mudah diterapkan untuk mencari koefisien binomial yaitu dengan menggunakan Konsep kombinasi $ C_r^n \, $ yang dinamakan
, sehingga segitiga pascal dapat ditulis sebagai berikut.
Konsep Binomial Newton (Ekspansi Newton)
Berikut adalah rumus Binomial Newton secara umum : $(a+b)^n = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \, \, $ atau $ (a+b)^n = C_0^n a^n + C_1^n a^{n-1}b + ... + C_{n-1}^nab^{n-1} + C_n^nb^n $ dengan $ n, \, r \, $ adalah bilangan asli.
Bentuk $ \displaystyle \sum_{r=0}^n \, $ disebut notasi sigma yang merupakan pejumlahan.
Berikut beberapa contoh notasi sigma :
$ \displaystyle \sum_{r=0}^3 r^2 = 0^2 + 1^2 + 2^2 + 3^3 $
$ \displaystyle \sum_{i=2}^5 (2i+1) = (2.2+1) + (2.3+1) + (2.4+1) + (2.5+1) $
$ \displaystyle \sum_{k=1}^9 (k^3 + k) = (1^3 + 1) + (2^3 + 2) + (3^3 + 3) + (4^3 + 4) + ... + (9^3 + 9) $
Contoh Soal Binomial Newton (Ekspansi Binomial) :
Untuk memudahkan menghitung bentuk kombinasi, silahkan baca materi kombinasi pada artikel "
1). Jabarkan bentuk binomial berikut ini:
d). $ \left( x + \frac{2}{x} \right)^5 $
a). $ (x+2)^4 \, $ artinya $ n = 4 $
$ \begin{align} (a+b)^n & = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \\ (x+2)^4 & = \displaystyle \sum_{r=0}^4 C_r^4 x^{4-r}2^r \\ & = C_0^4 x^{4-0}2^0 + C_1^4 x^{4-1}2^1 + C_2^4 x^{4-2}2^2 + C_3^4 x^{4-3}2^3 + C_4^4 x^{4-4}2^4 \\ & = 1. x^{4}.1 + 4. x^{3}.2 + 6. x^{2}.4 + 4. x^{1}.8 + 1. x^{0}.16 \\ (x+2)^4 & = x^{4} + 8x^{3} + 24 x^{2} + 32x + 16 \end{align} $
b). $ (2a + 3b)^3 \, $ artinya $ n = 3 $
$ \begin{align} (x+y)^n & = \displaystyle \sum_{r=0}^n C_r^n x^{n-r}y^r \\ (2a + 3b)^3 & = \displaystyle \sum_{r=0}^3 C_r^3 (2a)^{3-r}(3b)^r \\ & = C_0^3 (2a)^{3-0}(3b)^0 + C_1^3 (2a)^{3-1}(3b)^1 + C_2^3 (2a)^{3-2}(3b)^2 + C_3^3 (2a)^{3-3}(3b)^3 \\ & = 1. (2a)^{3} .1 + 3. (2a)^{2}(3b) + 3. (2a)^{1}(3b)^2 + 1. (2a)^{0}(3b)^3 \\ & = 1. 2^3.a^3 .1 + 3. 2^2.a^2.(3b) + 3. (2a).3^2.b^2 + 1. 1.3^3.b^3 \\ (2a + 3b)^3 & = 8a^3 + 36a^2b + 54ab^2 + 27b^3 \end{align} $
c). $ (a - 2b)^3 \, $ artinya $ n = 3 $
$ \begin{align} (x+y)^n & = \displaystyle \sum_{r=0}^n C_r^n x^{n-r}y^r \\ (a-2b)^3 & = (a + (-2b))^3 \displaystyle \sum_{r=0}^3 C_r^3 a^{3-r}(-2b)^r \\ & = C_0^3 a^{3-0}(-2b)^0 + C_1^3 a^{3-1}(-2b)^1 + C_2^3 a^{3-2}(-2b)^2 + C_3^3 a^{3-3}(-2b)^3 \\ & = 1. a^{3}.1 + 3. a^{2}(-2b) + 3. a^{1}(-2b)^2 + 1. a^{0}(-2b)^3 \\ & = a^{3} + 3. a^{2}(-2b) + 3. a.(-2)^2.b^2 + 1. 1.(-2)^3.b^3 \\ (a-2b)^3 & = a^{3} -6a^2b + 12ab^2 -8b^3 \end{align} $
d). $ \left( x + \frac{2}{x} \right)^5 \, $ artinya $ n = 5 $
$ \begin{align} (a+b)^n & = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \\ \left( x + \frac{2}{x} \right)^5 & = \displaystyle \sum_{r=0}^5 C_r^5 x^{5-r} \left( \frac{2}{x} \right)^r \\ & = C_0^5 x^{5-0} \left( \frac{2}{x} \right)^0 + C_1^5 x^{5-1} \left( \frac{2}{x} \right)^1 + C_2^5 x^{5-2} \left( \frac{2}{x} \right)^2 \\ & + C_3^5 x^{5-3} \left( \frac{2}{x} \right)^3 + C_4^5 x^{5-4} \left( \frac{2}{x} \right)^4 + C_5^5 x^{5-5} \left( \frac{2}{x} \right)^5 \\ & = 1. x^{5} .1 + 5. x^{4} \left( \frac{2}{x} \right) + 10. x^{3} \left( \frac{2^2}{x^2} \right) \\ & + 10. x^{2} \left( \frac{2^3}{x^3} \right) + 5. x^{1} \left( \frac{2^4}{x^4} \right) + 1. x^{0} \left( \frac{2^5}{x^5} \right) \\ & = x^5 + 5. x^{4} \left( \frac{2}{x} \right) + 10. x^{3} \left( \frac{4}{x^2} \right) \\ & + 10. x^{2} \left( \frac{8}{x^3} \right) + 5. x^{1} \left( \frac{16}{x^4} \right) + 1. x^{0} \left( \frac{32}{x^5} \right) \\ & = x^5 + 10 x^{3} + 40 x^{1} \\ & + 80 \left( \frac{1}{x} \right) + 80 \left( \frac{1}{x^3} \right) + \left( \frac{32}{x^5} \right) \\ \left( x + \frac{2}{x} \right)^5 & = x^5 + 10 x^{3} + 40 x + \frac{80}{x} + \frac{80}{x^3} + \frac{32}{x^5} \end{align} $
Menentukan Suku dan Koefisien Binomial
Dari rumus Binomial Newton berikut ini, $(a+b)^n = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \, \, $ Maka suku ke-$k$ bentuk suku banyak hasil penjabarannya dapat ditentukan dengan rumus : Suku ke-$k \, $ adalah $ \, C_{(k-1)}^n a^{n-(k-1)}b^{k-1} $.
Misalkan ada bentuk $ (2a + 3b)^3 \, $ yang bisa dijabarkan menjadi :
$ \begin{align} (2a + 3b)^3 & = 8a^3 + 36a^2b + 54ab^2 + 27b^3 \end{align} $
Suku-suku dari ekspansi binomial $ (2a + 3b)^3 \, $ adalah :
Suku ke-1 : $ \begin{align} 8a^3 \end{align} \, $ dengan koefisiennya 8.
Suku ke-2 : $ \begin{align} 36a^2b \end{align} \, $ dengan koefisiennya 36.
Suku ke-3 : $ \begin{align} 54ab^2 \end{align} \, $ dengan koefisiennya 54.
Suku ke-4 : $ \begin{align} 27b^3 \end{align} \, $ dengan koefisiennya 27.
Tentu kita tidak perlu menjabarkan sejara keseluruhan suku-sukunya jika hanya menentukan suku tertentu saja. Misalkan kita ingin mencari suku ke-2 dari bentuk binomial $ (2a + 3b)^3 \, $ , maka kita peroleh :
Suku ke-2 dengan $ k = 2 $ :
$ \begin{align} C_{(k-1)}^n x^{n-(k-1)}y^{k-1} & = C_{(2-1)}^3 (2a)^{3-(2-1)}(3b)^{2-1} \\ & = C_{1}^3 (2a)^{2}(3b)^{1} \\ & = 3. 4.a^2 .3b = 36a^2b \end{align} $.
artinya suke ke-2 dari binomial $ (2a + 3b)^3 \, $ adalah $ 36a^2b \, $ yang sesuai dengan bentuk di atasnya.
2). Tentukan suku ke-3 dari binomial $ (2x - 5y)^{20} \, $ dan besar koefisiennya.
*). Bentuk binomialnya : $ (2x - 5y)^{20} \, $ artinya $ n = 20 $.
*). Yang diminta suku ke-3 artinya $ k = 3 $.
Rumus suku ke-$k \, $ adalah $ \, C_{(k-1)}^n a^{n-(k-1)}b^{k-1} $ .
Suku ke-2 yaitu dari $ (2x - 5y)^{20} = (2x + (- 5y))^{20} \, $ :
$ \begin{align} C_{(k-1)}^n a^{n-(k-1)}b^{k-1} & = C_{(3-1)}^{20} (2x)^{20-(3-1)}(-5y)^{3-1} \\ & = C_{2}^{20} (2x)^{18}(-5y)^{2} \\ & = \frac{20!}{(20-2)!2!} . 2^{18}.x^{18}(-5)^2.y^{2} \\ & = \frac{20!}{18!2!} . 2^{18}.x^{18}.25.y^{2} \\ & = \frac{20.19.18!}{18!.2.1} . 2^{18}.x^{18}.25.y^{2} \\ & = \frac{20.19}{2} . 2^{18}.x^{18}.25.y^{2} \\ & = 190 . 2^{18}.x^{18}.25.y^{2} \\ & = (190 \times 2^{18} \times 25). x^{18}y^{2} \\ & = 4750 \times 2^{18} x^{18}y^{2} \end{align} $.
Sehingga suku ke-3 dari $ (2x - 5y)^{20} \, $ adalah $ \, 4750 \times 2^{18} x^{18}y^{2} \, $ dengan koefisiennya adalah $ 4750 \times 2^{18} $.
Untuk soal nomor 3 dan nomor 4 berikut gunakan beberapa sifat eksponen :
$ \frac{1}{a^n} = a^{-n} \, $ dan $ \, a^m . a^n = a^{m+n} $
3). Diketahi bentuk binomial $ (3a + b)^{50} \, $. Tentukan koefisien dari suku yang berbentuk $ a^{26}b^{24} \, $ dan terletak pada suku ke berapakah suku tersebut.
*). Bentuk $ (3a + b)^{50} \, $ , artinya $ n = 50 $.
*). Rumus suku ke-$k $ adalah $ C_{(k-1)}^n a^{n-(k-1)}b^{k-1} \, $ sehingga sama dengan $ a^{26}b^{24} $.
$ \begin{align} a^{n-(k-1)}b^{k-1} & = a^{26}b^{24} \\ a^{50-(k-1)}b^{k-1} & = a^{26}b^{24} \\ a^{50-(k-1)}b^{k-1} & = a^{26}b^{24} \end{align} $.
Dari persamaan terakhir di atas diperoleh : $ k - 1 = 24 \rightarrow k = 25 $.
Artinya bentuk $ a^{26}b^{24} \, $ adalah suku ke-25.
*). Menentukan koefisien suku ke-25 dengan $ k = 25 $ dari bentuk $ (3a + b)^{50} \, $
$ \begin{align} C_{(k-1)}^n x^{n-(k-1)}x^{k-1} & = C_{(25-1)}^{50} (3a)^{50-(25-1)}(b)^{25-1} \\ & = C_{24}^{50} (3a)^{26}(b)^{24} \\ & = C_{24}^{50} 3^{26}a^{26}b^{24} \end{align} $.
Jadi, koefisien dari bentuk $ a^{26}b^{24} \, $ adalah $ C_{24}^{50} \times 3^{26} $.
4). Diketahui bentuk binomial $ \left( x - \frac{1}{x} \right)^{2016} \, $ . Tentukan suku yang memuat bentuk $ x^{16} \, $ dan besar koefisiennya.
*). Bentuk $ \left( x - \frac{1}{x} \right)^{2016} \, $ , artinya $ n = 2016 $.
*). Rumus suku ke-$k $ adalah $ C_{(k-1)}^n a^{n-(k-1)}b^{k-1} \, $ sehingga sama dengan $ x^{16} $.
Bentuk $ \left( x - \frac{1}{x} \right)^{2016} = \left( x + (- \frac{1}{x} ) \right)^{2016} \, $ artinya $ a = x \, $ dan $ b = - \frac{1}{x} = -x^{-1} $.
$ \begin{align} a^{n-(k-1)}b^{k-1} & = x^{16} \\ x^{2016-(k-1)}\left( -x^{-1} \right)^{k-1} & = x^{16} \\ x^{2017-k} . (-1)^{k-1} . \left( x^{-1} \right)^{k-1} & = x^{16} \\ (-1)^{k-1} . x^{2017-k} . \left( x \right)^{1-k} & = x^{16} \\ (-1)^{k-1} . x^{(2017-k)+(1-k)} & = x^{16} \\ (-1)^{k-1} . x^{2018 - 2k} & = x^{16} \\ \end{align} $.
Dari persamaan terakhir di atas diperoleh : $ 2018 - 2k = 16 \rightarrow k = 1001 $.
Artinya bentuk $ x^{16} \, $ adalah suku ke-1001.
*). Menentukan koefisien suku ke-1001 dengan $ k = 1001 $ dari bentuk $ \left( x - \frac{1}{x} \right)^{2016} \, $
$ \begin{align} C_{(k-1)}^n a^{n-(k-1)}b^{k-1} & = C_{(1001-1)}^{2016} (x)^{2016-(1001-1)}(-x^{-1})^{1001-1} \\ & = C_{1000}^{2016} (x)^{1016}(-x^{-1})^{1000} \\ & = C_{1000}^{2016} (x)^{1016}(x^{-1})^{1000} \\ & = C_{1000}^{2016} (x)^{1016}(x)^{-1000} \\ & = C_{1000}^{2016} (x)^{1016 + (-1000)} \\ & = C_{1000}^{2016} x^{16} \end{align} $.
Jadi, koefisien dari bentuk $ x^{16} \, $ adalah $ C_{1000}^{2016} $.
Konsep Binomial Newton (Ekspansi Newton)
Berikut adalah rumus Binomial Newton secara umum : $(a+b)^n = \displaystyle \sum_{r=0}^n C_r^n a^{n-r}b^r \, \, $ atau $ (a+b)^n = C_0^n a^n + C_1^n a^{n-1}b + … + C_{n-1}^nab^{n-1} + C_n^nb^n $ dengan $ n, \, r \, $ adalah bilangan asli.
Keterangan : Bentuk $ \displaystyle \sum_{r=0}^n \, $ disebut notasi sigma yang merupakan pejumlahan. Berikut beberapa contoh notasi sigma : $ \displaystyle \sum_{r=0}^3 r^2 = 0^2 + 1^2 + 2^2 + 3^3 $ $ \displaystyle \sum_{i=2}^5 (2i+1) = (2.2+1) + (2.3+1) + (2.4+1) + (2.5+1) $ $ \displaystyle \sum_{k=1}^9 (k^3 + k) = (1^3 + 1) + (2^3 + 2) + (3^3 + 3) + (4^3 + 4) + … + (9^3 + 9) $